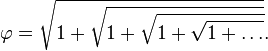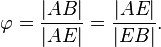Золотое сечение
26-06-2025, 01:33 . Разместил(а): vadimkrd
| Иррациональные числа γ - ζ(3) — √2 — √3 — √5 — φ — α — e — π — δ |
Золотое сечение (золотая пропорция, деление в крайнем и среднем отношении) — делениенепрерывной величины на две части в таком отношении, при котором меньшая часть так относится к большей, как большая ко всей величине.
Отношение большей части к меньшей в этой пропорции выражается квадратичной иррациональностью
и, наоборот, отношение меньшей части к большей
Число  называется также золотым числом.
называется также золотым числом.
В дошедшей до нас античной литературе деление отрезка в крайнем и среднем отношении (ἄκρος καὶ μέσος λόγος) впервые встречается в «Началах» Евклида (ок. 300 лет до н. э.), где оно применяется для построения правильного пятиугольника.
Лука Пачоли, современник и друг Леонардо да Винчи, называл это отношение «божественной пропорцией». Термин «золотое сечение» (goldener Schnitt) был введён в обиход Мартином Омом в 1835 году.
Золотое сечение имеет множество замечательных свойств, но ещё больше свойств вымышленных[1][2][3].
Содержание[убрать] |
[править]Математические свойства
 — иррациональное алгебраическое число, положительное решение квадратного уравнения
— иррациональное алгебраическое число, положительное решение квадратного уравнения  , откуда, в частности, следуют соотношения:
, откуда, в частности, следуют соотношения:
 — представляется через тригонометрические функции:
— представляется через тригонометрические функции:
 представляется в виде бесконечной цепочки квадратных корней:
представляется в виде бесконечной цепочки квадратных корней:
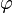 представляется в виде бесконечной цепной дроби
представляется в виде бесконечной цепной дроби
- подходящими дробями которой служат отношения последовательных чисел Фибоначчи
 . Таким образом,
. Таким образом,
-
- Мера иррациональности
 равна 2.
равна 2.
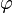 является знаменателем геометрической прогрессии, каждый член которой, начиная с третьего, равен сумме двух предыдущих.
является знаменателем геометрической прогрессии, каждый член которой, начиная с третьего, равен сумме двух предыдущих.
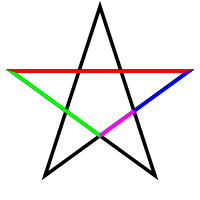
- В правильной пятиконечной звезде каждый отрезок делится пересекающим его отрезком в золотом сечении (на приведённом рисунке отношение красного отрезка к зелёному, так же как зелёного к синему, так же как синего к фиолетовому, равны
 ).
).
- Геометрическое построение. Золотое сечение отрезка
 можно построить следующим образом: в точке
можно построить следующим образом: в точке  восстанавливают перпендикуляр к
восстанавливают перпендикуляр к  , откладывают на нём отрезок
, откладывают на нём отрезок 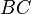 , равный половине
, равный половине  , на отрезке
, на отрезке  откладывают отрезок
откладывают отрезок 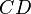 , равный
, равный 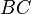 , и наконец, на отрезке
, и наконец, на отрезке  откладывают отрезок
откладывают отрезок 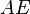 , равный
, равный  . Тогда
. Тогда
- Отношение диагонали правильного пятиугольника к стороне равно золотому сечению.
[править]Золотое сечение и гармония в искусстве
Под «правилом золотого сечения» в архитектуре и искусстве обычно понимаются асимметричные композиции, не обязательно содержащие золотое сечение математически.
Есть основание считать, что значимость золотого сечения в искусстве преувеличена и основывается на ошибочных расчётах. Некоторые из таких утверждений:
- Пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона якобы свидетельствуют, что египетские мастера пользовались соотношениями золотого сечения при их создании.
- Согласно Ле Корбюзье, в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют золотому сечению. В фасаде древнегреческого храма Парфенона также присутствуют золотые пропорции. В циркуле из древнеримского города Помпеи (музей в Неаполе) также заложены пропорции золотого деления, и т. д. и т. п.
При обсуждении оптимальных соотношений сторон прямоугольников (размеры листов бумаги A0 и кратные, размеры фотопластинок (6:9, 9:12) или кадров фотоплёнки (часто 2:3), размеры кино- и телевизионных экранов — например, 3:4 или 9:16) были испытаны самые разные варианты. Оказалось, что большинство людей не воспринимает золотое сечение как оптимальное и считает его пропорции «слишком вытянутыми».
[править]Примеры сознательного использования
Начиная с Леонардо да Винчи, многие художники сознательно использовали пропорции «золотого сечения». Российский зодчий Жолтовский также использовал золотое сечение в своих проектах[4].
Известно, что Сергей Эйзенштейн искусственно построил фильм «Броненосец Потёмкин» по правилам золотого сечения. Он разбил ленту на пять частей. В первых трёх действие развивается на корабле. В двух последних — в Одессе, где разворачивается восстание. Этот переход в город происходит точно в точке золотого сечения. Да и в каждой части есть свой перелом, происходящий по закону золотого сечения. В кадре, сцене, эпизоде происходит некий скачок в развитии темы: сюжета, настроения. Эйзенштейн считал, что, так как такой переход близок к точке золотого сечения, он воспринимается как наиболее закономерный и естественный.
[править]См. также
- Пифагорейский пентакл
- Фибоначчиева система счисления
- Правило третей
- Метод золотого сечения
- Квадратный корень из 5 → Золотое сечение